Alexey Onufriev
Blacksburg, VA 24061
M.S. Biophysics, Moscow Institute of Physics and Technology
Ph.D. Computational Solid State Physics, Brown University
Our group develops and uses theoretical and computational methods to understand dynamics and function of biomolecular systems such as proteins, DNA, and their complexes. The computations are often performed on supercomputers. My philosophy is that among the multitude of models of a complex system that one can build, only the very simple, robust solutions may have a chance to represent reality. Complex solutions with tens of fitting parameters may sometimes be of great practical use, but often misrepresent reality (the geocentric model of the Universe is one such example). The same philosophy applies to computational methods we develop: simple, robust solutions are preferred. As with any theoretical work, close contact with experimental groups is essential.
We work at the interface of physics, biology, and computer science; the research is a collective effort of our group members who have background in one or more of these fields. Specific projects range from those based on analytical techniques that require no computation, to ones where computation on highly parallel clusters is essential. The funding comes from the NIH and the NSF. Active Research Areas
BIMOLECULAR ELECTROSTATICS
Long-range electrostatic interactions play crucial role in determining biological properties of macromolecules. However, since realistic biomolecular shapes are very complex, modeling the effects of these interactions is difficult, both from conceptual and computational points of view. We work on developing several models that address the problem. We apply the models to understand biological functions that depend critically on electrostatics.
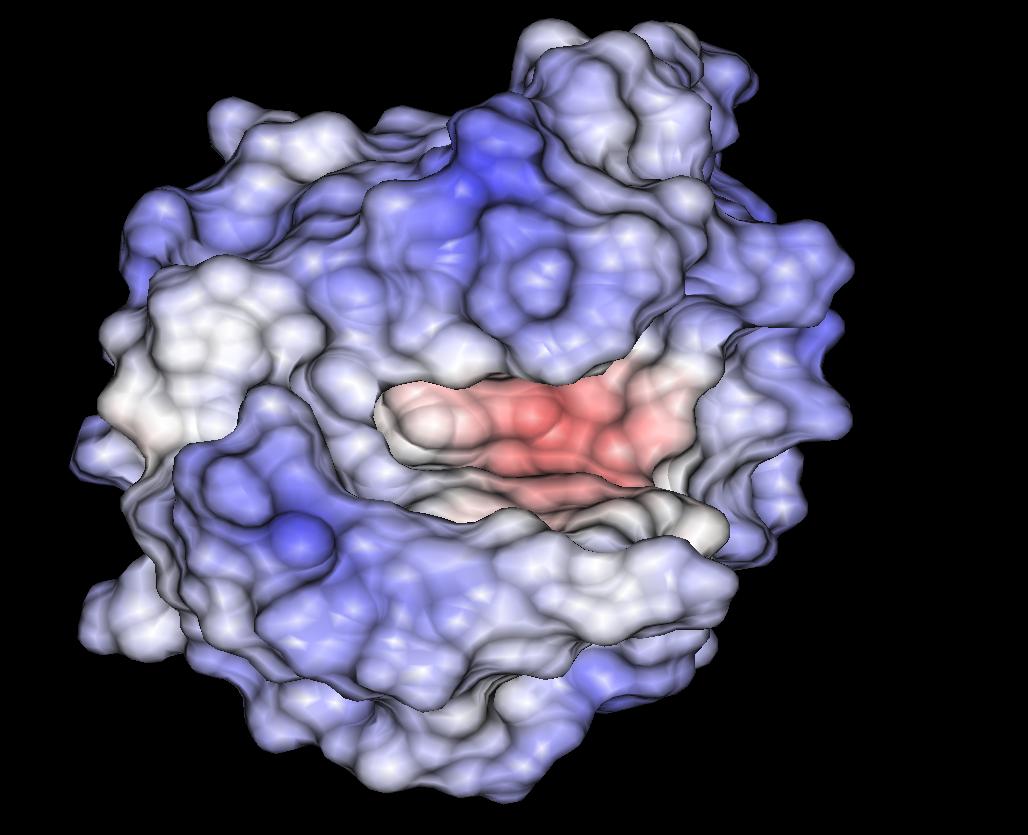Electrostatic potential computed in the active pocket of protein lysozyme. Pictures like this one often help to understand how biological macromolecules function.
EXAMPLE PUBLICATIONS:
Andrew T. Fenley, David A. Adams, and Alexey V. Onufriev Charge State of the Globular Histone Core Controls Stability of the Nucleosome. Biophysical Journal, 99 , 1577-1585 (2010).
Andrew T. Fenley, John C. Gordon, and A. Onufriev, An Analytical Approach to Computing Biomolecular Electrostatic Potential, I: Derivation and Analysis. Journal of Chemical Physics, 129, 075101, 2008.
Aguilar B, Anandakrishnan R, Ruscio JZ, Onufriev AV, Statistics and Physical Origins of pK and Ionization State Changes upon Protein-Ligand Binding Biophysical Journal, 98 , 872-880, 2010.
EXAMPLE PROJECTS:
Making molecular simulations run faster
EXAMPLE PUBLICATIONS:
Ramu Anandakrishnan, Tom Scogland, Andrew Fenley, John Gordon, Wu Feng and Alexey V. Onufriev. Accelerating Electrostatic Surface Potential Calculation with Multiscale Approximation on Graphics Processing Units. Journal of Molecular Graphics and Modelling, 28(8), 904-910, 2010.
Ramu Anandakrishnan and Alexey V. Onufriev. An N log N approximation based on the natural organization of biomolecules for speeding up the computation of long range interactions , Journal of Computational Chemistry, 31(4), 691–706, 2010.
EXAMPLE PROJECTS:
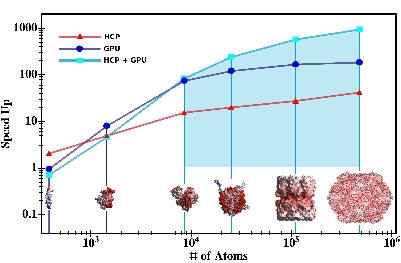
Long range electrostatic interactions play a critical role in thestructure, function and activity of biological molecules. However the modeling of electrostatic interactions is computationally intensive, making it impractical to simulate realistic systems for useful time-scales, even with today's fastest supercomputers. We have developed a novel method, hierarchical charge partitioning (HCP),for speeding up such computations. HCP has been implemented in the open source molecular dynamics software NAB in Amber tools to deliver up to 3 orders of magnitude speedup. HCP has also been ported to the GPU platfor m (ATI and nvidia) for an additional 1-2 orders of magnitude speedup.
Compaction and flexibility of the DNA
Recently, an intriguing new phenomenon was reported experimentally [see works of J. Widom's group]: on short length scales (~ 100 b.p.) DNA double helix does not behave as a relatively stiff rod, as might be expected based on its conventional persistence length value of ~ 150 b.p. In contrast, short DNA fragments were found to cyclize spontaneously, with an appreciable probability. Exactly how this unusual flexibility is accommodated structurally is not known. Since relatively short, bent DNA fragments participate in many vital biological processes, the issue is important. We use large-scale molecular dynamics simulations to understand the mechanism behind the phenomenon.
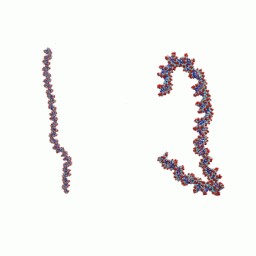The bending of the nucleosomal DNA observed in our simulations.
This movie shows a 5 ns MD simulation of the nucleosomal DNA (146 bp) at 300K in implicit solvent. To facilitate visual analysis of the structural features, the actual trajectory is played repeatedly many times. Due to the absence of viscosity, the 5ns of the actual simulation time corresponds to a much larger real time, probably in the hundreds of ns. For details, see J. Zmuda and A. Onufriev, ``A computational study of nucleosomal DNA flexibility", Biophys. J. 2006. The authors thank TIZBI, Inc. for the help with the animation and artistic rendering issues.
Understanding the function of the nucleosome
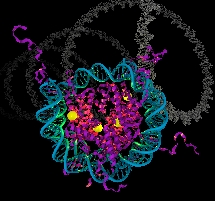Structure of the nucleosome (left) and the predicted diagram of its stability (right).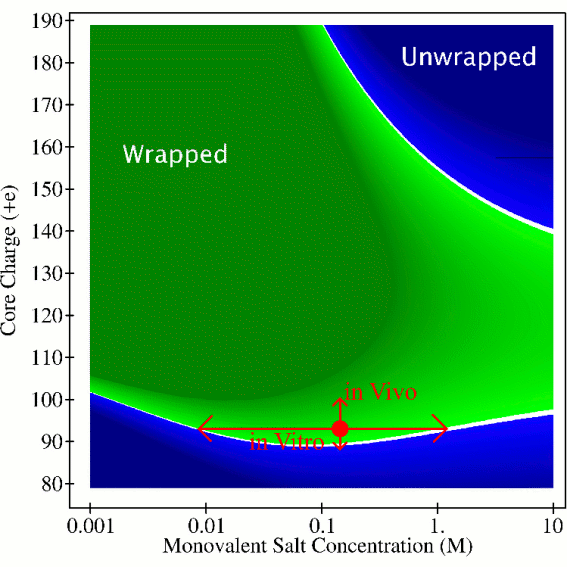 
Evidence is now overwhelming that not only the sequence, but also the details of DNA packaging inside the cell are an important part of the genetic message. The primary level of DNA compaction in eukareotic organisms in vivo is the nucleosome . At this level, a stretch of 147 base-pairs of the DNA is tightly wrapped 1.65 times around a set of eight proteins that carry the charge opposite of that of the DNA. Details of the nucleosome dynamics are vital for understanding key cellular processes such as DNA replication, repair and transcription. Cell differentiation is also intimately linked with DNA compaction. Despite its importance, the nucleosome system is far from being fully understood. One of the key unanswered questions is the following: how can the whole nucleosome be highly stable, protective of its genetic material, while at the same time its tightly wrapped DNA be highly accessible, easily revealing its information content? We have developed a theoretical model ( Andrew T. Fenley, David A. Adams, and Alexey V. Onufriev. ``Charge State of the Globular Histone Core Controls Stability of the Nucleosome" Biophysical Journal, 99, 1577-1585 (2010)) that addresses these issues.
Understanding ion-mediated compaction of nucleic acids
Ions play essential roles in governing the structure and function of nucleic acids, due to the large negative charge associated with the nucleic acid backbone. The addition of even small amounts of multivalent, positively charged (or counter-) ions induces inter- helix attraction in DNA and thus efficiently packages the extended polymer(s) into compact toroids. In vivo, the ion-mediated interactions are critical to proper compaction and function of DNA in the chromatin. Similar physical processes are responsible for packaging DNA into viral capsids. Mean-field theories do not account for the correlations that appear to be important for ion-mediated NA-NA attraction, and the standard “electrostatics only” PB approach misses many other physically relevant effects. Models that go beyond mean-field have been developed and provided general insights into the physics of the ion-mediated DNA attraction. However, to make progress, these approaches rely on drastic approximations to NA shape (perfect cylinder, sphere) and/or simplified interaction potentials (e.g. scaled Coulomb). As a result, they cannot provide the detailed picture we seek. Fully explicit solvent simulations could, in principle, provide the right level of detail, but they often face prohibitive sampling issues in these strongly correlated, highly charged systems. These limitations become especially severe in the case of biologically important, but more structurally complex, charged polyamines such as spermine and spermidine essential for cell function. The absence of efficient computational models that adequately describe the multivalent ion – NA system hinders progress in areas fundamental to biomedical science (outlined above) that need detailed understanding of the process of DNA or RNA compaction and interaction induced by multivalent ions and charged polyamines. We combine the efforts of three research groups to pioneer a new and tightly integrated approach that will bridge various levels of theory and experiment with the goal of understanding ion-induced nucleic acid interactions.
The role of "boundary conditions" in the 3D genome architecture
3D nuclear architecture is vital to genome function, however its underlying principles are only beginning to emerge. This collaborative project (with I. Sharakhov, entomology) aims to uncover the fundamental mechanisms of maintaining nuclear architecture via interactions between chromosomes and the nuclear envelope (NE) – an area almost unexplored. Specifically, investigate the role of the “boundary conditions” -- chromosome–NE attachments -- in establishing intra- and inter-chromosomal contacts. Solving this problem will significantly improve our understanding of the role of nuclear architecture in regulation of gene expression, DNA double-strand break repair, generation of chromosomal rearrangements, and, ultimately, epigenetic inheritance.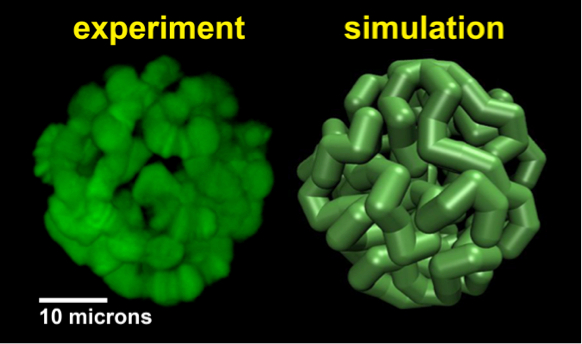 
Modeling of giant (polytene) chromosomes in fruit fly
Building the 3D genome, one nucleosome at a time.
In this highly colaborative project (with several institutes in St. Petersburg, Russia) we are trying to reconstruct the entire 3D genome using two approaches:
1. Top-down: Small Angle Neutron Scattering.
2. Bottom-up: Atomistic modeling.
PROTEIN FOLDING
One of the large challenges in modern science is working out how proteins curl up into their complex shapes. They do this in fractions of a second, always adopting the same three-dimensional form. And while we have, for the past fifty years, known the exact rule that uniquely determines the amino-acid sequence of a protein from the corresponding DNA sequence, the second part of the genetic code, that is the ability to determine the full 3D structure of the protein from its amino-acid sequence, is still missing. This is the essence of the so-called "protein folding problem": given an amino-acid sequence how does one predict the 3D shape that this protein will take upon folding? Since it is this shape that ultimately determines the biological function of a protein, solving the problem is of great importance.
EXAMPLE PROJECTS:
PROTEIN DYNAMICS
EXAMPLE PUBLICATIONS:
Jory Z. Ruscio, Deept Kumar, Maulik Shukla, Michael G. Prisant, T. M. Murali, and Alexey V. Onufriev, Atomic level computational identification of ligand migration pathways between solvent and binding site in myoglobin , Proceedings of the National Academy of Sciences, (USA), 15, 9204-9209 (2008).
EXAMPLE PROJECTS:
Exactly how does oxygen, and other small non-polar ligands such as CO get to the buried binding site in myoglobin?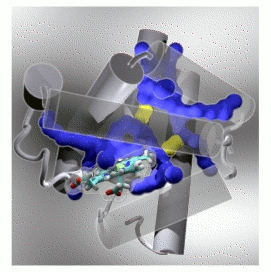 
Dynamic pathways for ligand migration between solvent and binding site in the oxygen storage protein myoglobin. Pathways and connecting gateways determined by molecular dynamics simulation are respectively shown in blue and yellow. Protein helical structural elements and connecting loops are represented by grey colored cylinders and rope. The heme binding site -- buried and inaccessible to solvent in the static structure -- is shown as a stick figure model.
THEORY OF COOPERATIVE LIGAND BINDING
Binding of ligands to macromolecules is one of the most important reactions in biology; well-known examples include oxygen binding to hemoglobin or binding of protons to titratable groups in proteins. The binding curves may often appear deceptively featureless, yet the underlying microscopic models may be rather complex, and connections between them not intuitive.
A novel view on titration of biomolecules.
When individual titratable sites in a molecule interact with each other, their pH-titration can be considerably more complex than that of an independent site described by the classical Henderson-Hasselbalch equation. We propose a novel framework - the Decoupled Sites Representation - that decomposes any complex titration behavior into simple standard components. The approach maps the set of N interacting sites in the molecule onto a set of N independent, non-interacting quasi-sites, each characterized by a pK' value. The titration curve of an individual site in the molecule is a weighted sum of Henderson-Hasselbalch curves corresponding to the quasi-sites. The total protonation curve is the unweighted sum of these Henderson-Hasselbalch curves. We show that pK' values correspond to deprotonation constants available from methods that measure total proton uptake or release, and establish their connection to protonation curves of individual residues obtained by NMR or infra-red spectroscopy. The new framework is tested on a small molecule diethylene-triamine-penta-acetate (DTPA) exhibiting non-monotonic titration curves, where it gives an excellent fit to experimental data. We demonstrate that the titration curve of a site in a group of interacting sites can be accurately reconstructed, if titration curves of the other sites are known. The application of the new framework to the protein rubredoxin demonstrates its usefulness in calculating and interpreting complicated titration curves.
APPLICATION: Titration of DTPA.
-
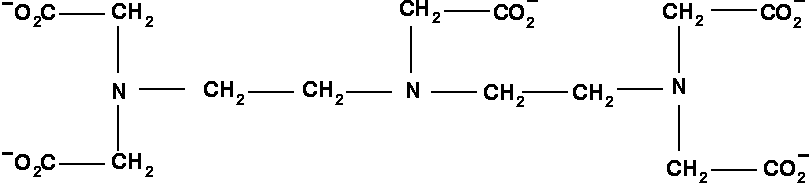
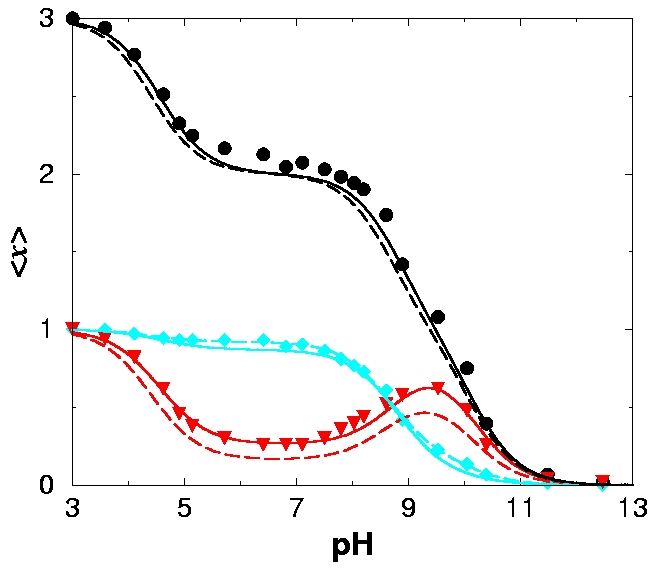
Note that fitting the seemingly featureless titration curves of the terminal nitrogens allows on to reconstruct the non-trivial titration behavior of the middle nitrogen.
Biochemistry, ("New Concepts") 40,
BACTERIORHODOPSIN
Proton-pumping mechanism
Bacteriorhodopsin is the smallest autonomous light-harvesting protein that transforms the energy of light into that of transmembrane H+ gradient. It is arguably the simplest and best understood of all known active transport systems, and has been the focus of intensive biophysical and structural studies aimed at understanding its mechanism in atomic detail. Despite almost 30 years of intense research, there is still no unifying quantitative model of proton transfer in bacteriorhodopsin describing the entire photocycle. The ability of this molecular machine to pump protons effeciently in one direction, from the cytoplasmic to the extracellular side of the cell membrane, depends on concerted changes of charge states of only a small group of key residues, which makes it an attractive problem for a physicist.
Strong electrostatic interactions (up to 25 kT ) between the key titratable groups make the traditional description in terms of single-site pKs inappropriate; a full many-body description in terms of protonation states is necessary.
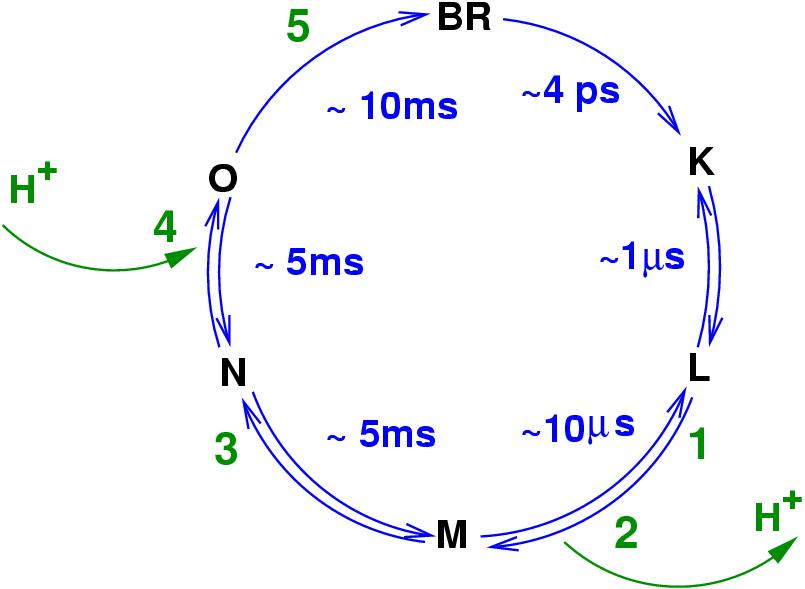
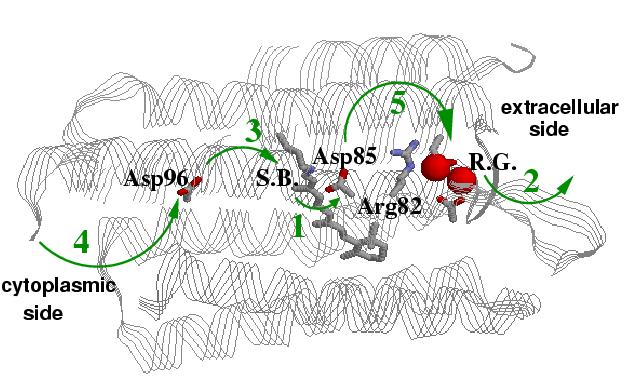
Left: A diagram of the bacteriorhodopsin photo-cycle showing transitions between conformational states. Absorption of a photon in the ground (BR) state leads to isomerization of the retinal Schiff base (S.B.) form all-trans to 13-cis in the K intermediate. After further relaxation to L, the proton transfer begins with the onset of the M state.
Right: A structure of bacteriorhodopsin showing key residues directly invoved in sequential proton transfer events (1 through 5) coupled to conformational changes: 1 -- protonation of Asp85 from the Schiff Base (S.B.); 2 -- proton release to the extracellular side; 3 -- reprotonation of the Schiff base from Asp96; 4 -- uptake of a proton form the cytoplasmic side (left) by Asp96; 5 -- proton transfer from Asp85 to the release group (R.G.), which is believed to involve Glu194, Glu204 and a H5O2+ cluster.
E-mail: onufriev@cs.vt.edu
Insights into the mechanisms of RNAi
RNA interference (RNAi) is a phenomenon of gene silencing at the mRNA level offering a quick and easy way to determine the function of a gene both in vivo and in vitro. Onufriev's group is a part of multi-disciplinary, multi-institutional team who is trying to develop quantitative models of the process. Our group is looking into the problem at the level of atomic-resolution structures.
Refereed publications. As of 08/17, the total number of citations is 11000. Source: Google Scholar. 68. Negin Forouzesh, Saeed Izadi, and Alexey V. Onufriev ``Grid-based Surface Generalized Born Model for Calculation of Electrostatic Binding Free Energies", Journal of Chemical Information and Modeling, in press (2017). 67. A. Gabrieli, M. Sant, S. Izadi, P.S. Shabane, A.V. Onufriev, G.B. Suffritti ``High-Temperature Dynamic Behavior in Bulk Liquid Water: A Molecular Dynamics Simulation Study using the OPC and TIP4P-Ew Potentials", Frontiers of Physics 13, 138203 (2017). 66. Ekaterina Katkova, Alexey V. Onufriev, Boris Aguilar, and Vladimir B. Sulimov ``Accuracy comparison of several common implicit solvent models and their implementations in the context of protein-ligand binding", Journal of Molecular Graphics and Modelling, 72, 70-80 (2017). 65. Andrea M Katz, Igor S Tolokh, Suzette A Pabit, Nathan Baker, Alexey V Onufriev, Lois Pollack ``Spermine condenses DNA, but not RNA duplexes", Biophysical Journal, 112, 22-30, (2017). 64. Ramu Anandakrishnan, Mayank Daga, Alexey Onufriev, and Wu Feng ``Multiscale Approximation with Graphical Processing Units for Multiplicative Speedup in Molecular Dynamics", Proceedings of the 7th ACM Conference on Buoinformatics, Computational Biology, and Health Informatics, Seattle, WA, October (2016). 63. Georgy N. Rychkov, Andrey V. Ilatovskiy, Igor Nazarov, Alexei Shvetsov, Dmitry Lebedev, Alexander Konev, Vladimir Isaev-Ivanov, and Alexey. V. Onufriev “Partially assembled nucleosome structures at atomic detail", Biophysical Journal, 112, 46-472, (2016). 62. Saeed Izadi, Ramu Anandakrishnan*, and Alexey V. Onufriev “Implicit Solvent Model for Million-Atom Atomistic Simulations: Insights into the Organization of 30-nm Chromatin Fiber", Journal of Chemical Theory and Computation, 12, pp 5946–5959, (2016). 61. Saeed Izadi and A.V. Onufriev ``Accuracy Limit of Rigid 3-point Water Models", J. Chem. Phys., 145, 074501 (2016). 60. Alexander Drozdetski, Igor S. Tolokh, Lois Pollack, Nathan Baker , and Alexey V. Onufriev, “Opposing effects of multivalent ions on flexibility of DNA and RNA”, Physical Review Letters, 117, 028101 (2016). 59. Suzette A Pabit, Andrea M Katz, Igor S Tolokh, Aleksander Drozdetski, Nathan Baker, Alexey V Onufriev, Lois Pollack ``Understanding Nucleic Acid Structural Changes by Comparing Wide-Angle X-ray Scattering (WAXS) Experiments to Molecular Dynamics Simulations", J. Chem. Phys. 144, 205102 (2016). 58. I.S. Tolokh, A.V. Drozdetski, L. Pollack, N.A. Baker, and A.V. Onufriev ``Multi-shell model of ion-induced nucleic acid condensation", J. Chem. Phys., 144, 155101 (2016). 57. Maria L. Sushko, Dennis G. Thomas, Suzette A. Pabit, Lois Pollack, Alexey V. Onufriev, Nathan A. Baker ``The Role of Correlation and Solvation in Ion Interactions with B-DNA", Biophysical Journal, 110, 315-326 (2016). 56. Saeed Izadi, Boris Aguilar, Alexey V. Onufriev ``Protein–Ligand Electrostatic Binding Free Energies from Explicit and Implicit Solvation", J. Chem. Theory and Comput., 11, 4450-4459 (2015). 55. Nicholas A. Kinney, Igor Sharakhov, and Alexey V. Onufriev ``Quantified effects of chromosome-nuclear envelope attachments on 3D organization of chromosomes", Nucleus, 6, 212-224 (2015). 54. Abhishek Mukhopadhyay, Igor S. Tolokh, and Alexey V. Onufriev ``Accurate Evaluation of Charge Asymmetry in Aqueous Solvation", Journal of Physical Chemistry (B) 119, 6092–6100 (2015). 53. Ramu Anandakrishnan, Aleksander Drozdetski, Ross Walker, and Alexey V. Onufriev ``Speed of conformational change: comparing explicit and implicit solvent molecular dynamics simulations", Biophysical Journal 108, 1153-64 (2015). 52. Saeed Izadi, Ramu Anandakrishnan and Alexey V. Onufriev ``Building Water Models, a Different Approach", J. Chem. Phys. Lett. 5, 3863-3871 (2014). 51. Igor S. Tolokh, Suzette A. Pabit, Andrea M. Katz, Yujie Chen, Aleksander Drozdetski, Nathan Baker, Lois Pollack, and Alexey V. Onufriev ``Why double-stranded RNA resists condensation", Nucleic Acids Research, 42, 10823-10831 (2014). 50. Abhishek Mukhopadhyay, Boris Aguilar, Igor S. Tolokh, and Alexey V. Onufriev ``Introducing Charge Hydration Asymmetry into the Generalized Born Model", J. Chem. Theory and Comput., 10 1788–1794 (2014). 49. Alexey V. Onufriev and Boris Aguilar ``Accuracy of continuum electrostatic calculations based on three common dielectric boundary definitions.", J. Theor. and Comput. Chemistry, 13, 1440006 (2014). 48. Nicholas A. Kinney, Igor Sharakhov, and Alexey V. Onufriev. "Investigation of the chromosome regions with significant affinity for the nuclear envelope in fruit fly – a model based approach", PLOS One, 9, e91943 (2014). 47. Anandakrishnan R, Baker C, Izadi S, Onufriev AV. ``Point Charges Optimally Placed to Represent the Multipole Expansion of Charge Distributions, PLOS One, 8, e6771 (2013). 46. Alexey V. Onufriev and Emil Alexov. ``Protonation and pK changes in protein-ligand binding", Quarterly Review of Biophysics, 46, 181-209 (2013). 45. Alexander V. Savin, Mikhail A. Mazo, Irina P. Kikot, and Alexey V. Onufriev. ``Two-phase stretching of molecular chains", Proceedings of the National Academy of Sciences, USA, 110, 2816-2821 (2013). 44. B. Aguilar and A.V. Onufriev. ``Efficient Computation of the Total Solvation Energy of Small Molecules via the R6 Generalized Born Model". J. Chem. Theory and Comput., 8, 2404-2411 (2012). 43. Abhishek Mukhopadhyay, Andrew T. Fenley, Igor S. Tolokh, and Alexey V. Onufriev. ``Charge Hydration Asymmetry: The Basic Principle and How to Use It to Test and Improve Water Models". Journal of Physical Chemistry (B), 116 9776–9783 (2012). 42. Ramu Anandakrishnan, Boris Aguilar and Alexey V. Onufriev. ``H++ 3.0: automating pK prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulation". Nucleic Acids Research, 40(W1), 537-541 (2012). 41. I.P Kikot, A.V. Savin, E.A. Zubova, M.A. Mazo, E.B. Gusarova, L.I. Manevitch, and A.V. Onufriev. ``New Coarse-Grained DNA Model", Biophysics, 56, 387-392 (2011). 40. Alexander V. Savin, Mikhail A. Mazo, Irina P. Kikot, Leonid I. Manevitch, and Alexey V. Onufriev. ``Heat conductivity of the DNA double helix", Phys. Rev. B 83, 245406 (2011). 39. Onufriev, A. V., and Sigalov, G. ``A strategy for reducing gross errors in the generalized Born models of implicit solvation", The Journal of Chemical Physics, 134, 164104, (2011). 38. Ramu Anandakrishnan, Mayank Daga, and Alexey V. Onufriev. ``An n log n Generalized Born Approximation", J. Chem. Theory and Comput. 7, 544-559 (2011). 37. Boris Aguilar, Richard Shadrach, and Alexey V. Onufriev. ``Reducing the Secondary Structure Bias in the Generalized Born Model via R6 Effective Radii", J. Chem. Theory and Comput., 6, 3613–3630 (2010). 36. Andrew T. Fenley, David A. Adams, and Alexey V. Onufriev. ``Charge State of the Globular Histone Core Controls Stability of the Nucleosome" Biophysical Journal, 99, 1577-1585 (2010). 35. Anandakrishnan R, Scogland TR, Fenley AT, Gordon JC, Feng WC, Onufriev AV. ``Accelerating electrostatic surface potential calculation with multi-scale approximation on graphics processing units", J. Mol. Graph. Model., 28, 904-910 (2010). 34. Nathan J. Palpant, Evelyne M. Houang, Wayne Delport, Kenneth E. M. Hastings, Alexey V. Onufriev, Yuk Y. Sham, and Joseph M. Metzger. ``Pathogenic peptide deviations support a model of adaptive evolution of chordate cardiac performance by troponin mutations", Physiol. Genomics, 42, 287-299, (2010). 33. Onufriev, Alexey. ``Continuum Electrostatics Solvent Modeling with the Generalized Born Model", pp. 127--165. In: Modeling Solvent Environments. Editor: M. Feig. Publisher: Wiley (2010). 32. Aguilar B, Anandakrishnan R, Ruscio JZ, Onufriev AV, ``Statistics and Physical Origins of pK and Ionization State Changes upon Protein-Ligand Binding", Biophysical Journal, 98, 872-880 (2010). 31. Ramu Anandakrishnan and Alexey V. Onufriev, ``An N log N approximation based on the natural organization of biomolecules for speeding up the computation of long range interactions", Journal of Computational Chemistry, 31, 691-706 (2010). 30. Bhattacharjee, P., N. Ramakrishnan, L. S. Heath, and A. V. Onufriev, ``Correlation Between Computed Equilibrium Secondary Structure Free Energy and siRNA Efficiency", IEEE International Conference on Bioinformatics and Biomedicine, Washington, DC, 351–351, (2009) 29. A. Onufriev, ``Implicit Solvent Models in Molecular Dynamics Simulations", Annual Reports in Computational Chemistry, 4, 125-137 (2008). PDF 28. John C. Gordon, Andrew T. Fenley, and A. Onufriev, ``An Analytical Approach to Computing Biomolecular Electrostatic Potential, II: Validation and Applications", Journal of Chemical Physics, 129, 075102 (2008). PDF 27. Andrew T. Fenley, John C. Gordon, and A. Onufriev, ``An Analytical Approach to Computing Biomolecular Electrostatic Potential, I: Derivation and Analysis", Journal of Chemical Physics, 129, 075101 (2008). PDF 26. Jory Z. Ruscio, Deept Kumar, Maulik Shukla, Michael G. Prisant, T. M. Murali, and Alexey V. Onufriev, ``Atomic level computational identification of ligand migration pathways between solvent and binding site in myoglobin", Proceedings of the National Academy of Sciences, (USA), 15, 9204-9209 (2008). 25. Ramu Anandakrishnan and Alexey Onufriev, ``Analysis of Basic Clustering Algorithms for Numerical Estimation of Statistical Averages in Biomolecules", Journal of Computational Biology, 15, 165-184 (2008). 24. J. Mongan, A. Svrcek-Seiler, and A. Onufriev, ``Analysis of integral expressions for effective Born radii", J. Chem. Phys. 127, 185101 (2007). PDF 23. J. Mongan, C Simmerling, J.A. McCammon, D.A. Case, and A. Onufriev, `` Generalized Born Model with a Simple, Robust Molecular Volume Correction ", J. Chem. Theory and Comput., 3, 156-169 (2007). PDF 22. N. Saha, L. T. Watson, K. Kafadar, N. Ramakrishnan, A. Onufriev, S. P. Mane, and C. Vasquez-Robinet, "Validation and estimation of parameters for a general probabilistic model of the PCR process'', J. Comput. Biology, 14, 102--117 (2007) 21. J. Z. Ruscio and Alexey Onufriev, "A Computational Study of Nucleosomal DNA Flexibility", Biophys. J., 91, 4121-4132 (2006). PDF 20. N. Saha, L. T. Watson, K. Kafadar, A. Onufriev, N. Ramakrishnan, C. Vasquez-Robinet, and J. Watkinson, ``A general probabilistic model of the PCR process'', Appl. Math. Comput., 182, 232--243, (2006) 19. Myers J, Grothaus G, Narayanan S, Onufriev A, "A simple clustering algorithm can be accurate enough for use in calculations of pKs in macromolecules", Proteins, 63, 928-938 (2006). PDF 18. G. Sigalov, A. Fenley, and A. Onufriev, "Analytical Linearized Poisson--Boltzmann Approach: Beyond the Generalized Born Approximation", J. Chem. Phys., 124, 124902 (2006). PDF 17. David A. Case, Thomas E. Cheatham III, Tom Darden, Holger Gohlke, Ray Luo, Kenneth M. Merz Jr., Alexey Onufriev, Carlos Simmerling, Bing Wang, Robert J. Woods, "The Amber biomolecular simulation programs", J. Comp. Chem., 26, 1668-1688 (2005). PDF 16. Gordon JC, Myers JB, Folta T, Shoja V, Heath LS and Onufriev A., "H++: a server for estimating pKas and adding missing hydrogens to macromolecules", Nucleic Acids Res. Jul 1;33:W368-71. (2005). PDF 15. G. Sigalov, P. Scheffel, and A. Onufriev, "Incorporating variable dielectric environments into the generalized Born model", J. Chem. Phys., 122, (2005). PDF 14. A. Onufriev and G. M. Ullmann, "Decomposing Complex Ligand Binding into Simple Components: Connections between Microscopic and Macroscopic models", J. Phys. Chem. B., 108, 11157-11169 (2004). PDF 13. M. Feig, A. Onufriev, M. S. Lee, W. Im, D. A. Case, C. L. Brooks, ``Performance Comparison of Generalized Born and Poisson Methods in the Calculation of Electrostatic Solvation Energies for Protein Structures", J. Comp. Chem , 468 , 96-111 (2004). PDF 12. Alexey Onufriev, D. Bashford and D.A. Case, "Exploring native states and large-scale conformational changes with a modified Generalized Born model.", Proteins, 55, 383-394 (2004). PDF 11. Alexey Onufriev, A. Smondyrev, and D. Bashford, ``Proton Affinity Changes Driving Unidirectional Proton Transport in the Bacteriorhodopsin Photocycle", J. Mol. Biol. 232 , 1183-1193 (2003). PDF 10. H. T. Allawi, M. W. Kaiser, Alexey Onufriev, Wu-Po Ma, A. E. Brogaard, D. A. Case, B. P. Neri and V. I. Lyamichev, "Modeling of Flap Endonuclease Interactions with DNA Substrate", J. Mol. Biol. 328 , 537-554 (2003). PDF 9. J. D. Hirst, S. Bhattacharjee, and Alexey Onufriev, Theoretical studies of time-resolved spectroscopy of protein folding", Faraday Discussions. 122, 253-267 (2003). PDF 8. Alexey Onufriev, D.A. Case, and D. Bashford, "Structural details, pathways, and energetics of unfolding apomyoglobin.``, J. Mol. Biol. 325, 555-567 (2003). PDF 7. Alexey Onufriev, D. Bashford and D.A. Case, "Effective Born radii in the generalized Born approximation: The Importance of Being Perfect.", J. Comp. Chem. 23, 1297-1304 (2002). PDF 6. Alexey Onufriev, D.A. Case and G. M. Ullmann, `` A Novel View of pH Titration in Biomolecules", Biochemistry, (``New Concepts") 40, 3413 (2001). PDF 5. Leduc SA, McAuley GA, Pentzell CB, Onufriev A, Lupton JH, Asllani I, Martin T. ``Physics passages and questions." In: MCAT in-class passage compendium. The Princeton Review: (2001). (textbook) 4. Alexey Onufriev, D. Bashford and D.A. Case ``A Modification of the Generalized Born Model Suitable for Macromolecules", J. Phys. Chem., 104, 3712 (2000). PDF 3. Alexey Onufriev and J.B. Marston, ``Enlarged Symmetry and Coherence in Arrays of Quantum Dots", Phys. Rev. B., 59, 12573 (1999). PDF 2. Alexey Onufriev and J.B. Marston, ``Memory Loss and Auger Processes in a Many-Body Theory of Charge Transfer", Phys. Rev. B. 53, 13340 (1996). PDF 1. Goldfeld, M.G, Lobysheva, I., Mikoyan, M.D., Chernavskii, D.S., and Onufriev A.V., ``ATP Synthesis By Free and Membrane-Bound H+ ATPase of the Chloroplasts in Conditions of a pH shift.", Biophysics 38, 1005 (1993). ABSTRACT
Software
Relaxed, atomistic structure of a 30nm chromatin fiber (40 nuncleosomes). Along with amber format topology and coordinate files for (multiresolution, HCP) MD simulation in implicit solvent. Details are in "Implicit Solvent Simulation of Million-Atom Structures: Insights into the Organization of 30-nm Chromatin Fiber" by Saeed Izadi, Ramu Anandakrishnan, and Alexey V. Onufriev, JCTC, (2016).
H++: Automated prediction of pK and protonation states in macromolecules. The web server computes pK values of ionizable groups in macromolecules and adds missing hydrogen atoms according to the specified pH of the environment. Given a (PDB) structure file on input, H++ outputs the completed structure in several common formats (PDB, PQR, AMBER inpcrd/prmtop) and provides a set of tools for analysis of electrostatic-related molecular properties. Details: Anandakrishnan R, Aguilar B, Onufriev AV. ``H++ 3.0: automating pK prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulations.", Nucleic Acids Res. 40, W537-41 (2012).
12CG. Coarse-grained Molecular Dynamics of the DNA. This is a set of programs to perform coarse-grained MD simulations and calculations of the DNA heat conductivity described in Alexander V. Savin, Mikhail A. Mazo, Irina P. Kikot, Leonid I. Manevitch, and Alexey V. Onufriev. ``Heat conductivity of the DNA double helix", Phys. Rev. B 83, 245406 (2011)
GBNSR6 (2.0, MSMS-based): Generalized Born and Charge Asymmetric Generalized Born solvation energies of molecules based on the R6 effective Born radii. Boris Aguilar, Richard Shadrach, and Alexey V. Onufriev. ``Reducing the Secondary Structure Bias in the Generalized Born Model via R6 Effective Radii", J. Chem. Theory and Comput., 6, 3613–3630 (2010). Mukhopadhyay et al. "Introducing Charge Hydration Asymmetry into the Generalized Born Model"
GEM (1.3): Computation and Visualization of Electrostatic Potential Around Biomolecules. John C. Gordon, Andrew T. Fenley, and A. Onufriev, ``An Analytical Approach to Computing Biomolecular Electrostatic Potential, II: Validation and Applications", Journal of Chemical Physics, 129, 075102 (2008)
PATHFINDER (beta 0.1): analysis of voids in macromolecules .
Jory Z. Ruscio, Deept Kumar, Maulik Shukla, Michael G. Prisant, T. M. Murali, and Alexey V. Onufriev, ``Atomic level computational identification of ligand migration pathways between solvent and binding site in myoglobin", Proceedings of the National Academy of Sciences, (USA), 15, 9204-9209 (2008).
Macromolecular Contacts Tool. Analysis of residue-residue contacts in biomolecules (proteins, DNA). A GUI-based JAVA (platform free ) code that computes and displays residue-residue contacts for multiple sets of macromolecular snapshots, e.g. coming from various MD trajectories.
Visualization of electrostatic interactions between titratable groups in proteins . Visualization (and some analysis) of clusters of electrostatically coupled groups and their interactions in proteins. A simple rasmol-based script.
Myers J, Grothaus G, Narayanan S, Onufriev A, "A simple clustering algorithm can be accurate enough for use in calculations of pKs in macromolecules", Proteins, 63, 928-938 (2006).
Calculation of pKs using a clustering algorithm .
Myers J, Grothaus G, Narayanan S, Onufriev A, "A simple clustering algorithm can be accurate enough for use in calculations of pKs in macromolecules", Proteins, 63, 928-938 (2006).
Estimation of the effective electrostatic size in the ALPB model .
G. Sigalov, P. Scheffe, and A. Onufriev, "Incorporating variable dielectric environments into the generalized Born model", J. Chem. Phys., 122, (2005);
G. Sigalov, A. Fenley, and A. Onufriev, "Analytical Linearized Poisson--Boltzmann Approach: Beyond the Generalized Born Approximation", J. Chem. Phys., 124, 124902 (2006)
DSRfit.1.1.beta.math. Example data. The DSR analysis of ligand binding curves. Currently available in the ``Mathematica" language. The code performs the analysis described in two separate publications:
1. Alexey Onufriev, D.A. Case and G. M. Ullmann, `` A Novel View of pH Titration in Biomolecules", Biochemistry, 40, 3413 (2001).
2. Alexey Onufriev and G. M. Ullmann, ``Decomposing Complex Cooperative Ligand Binding into Simple Components: Connections between Microscopic and Macroscopic models``, J. Phys. Chem , 108, 11157 (2004)